General Mathematics Previous Year Questions- 2018
GENERAL MATHEMATICS
SECTION-A
1. The number of decimal place after which the decimal expansion of the rational number 14588/625 will terminate is
(a) 2
(b) 3
(c) 4
(d) 5
Soln :-
Hence, The answer is (c) 4.
2. Which one of the following is a rational number?
(a) √2/√3
(b) √2/π
(c) √5/√6
(d) √3/√27
Soln :-$
3. The product of the zeros of 4u2 + 8u is
(a) 4
(b) 8
(c) 32
(d) 0
4u2 + 8u
⇒ 4u ( u + 2) = 0
Either, or,
4u = 0 u + 2 = 0
⇒ u = 0 ⇒ u = -2.
So, the product of the zeros of 4u2 + 8u is –
(-2) x 0 = 0.
The Answer is (d) 0.
4. Under what condition will ax2 + 5x + 7 = 0 be a quadratic equation?
(a) a > 0
(b) a < 0
(c) a = 0
(d) a ≠ 0
Soln :- (d) a ≠ 0.
5. In △ABC, ∠A = 90°, AB = 3 cm, BC = 5 cm and AD ⟂ BC. Then the length of AD is
(a) 5/2
(b) 12/5
(c) 5/12
(d) √39/2
6. The distance between the points (1, O) and (0, 1) is
(a) 2
(b) √2
(c) 1
(d) 0
Soln :- The distance between the points (1,0) and (0,1) is:-
7. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 45° The height of the tower is
(a) 30 m
(b) 15 m
(c) 10 m
(d) 60 m
Soln :-
⇒ BC = x = 30.
The Answer is (a) 30m
8. If the circumference of a circle is 22 cm, then the area of a quadrant of the circle is
(a) 77/8 cm2
(b) 77 cm2
(c) 77/2 cm2
(d) 77/4 cmcm2
Soln :- Here, the circumference (C) = 22 cm
Let, the radius = r cm.
According to the question,
the area of a quadrant of the circle is
9. The wickets taken by a bowler in 8 cricket matches are as follows
3, 2, 0, 1, 6, 2, 1, 2
The mode of the data is
(a) 3
(b) 6
(c) 2
(d) 1
Soln :- (c) The mode of the data is 2, as because 2 is repeated maximum time in the data.
10. The probability of an event ‘E’ + the probability of the event ‘not E’ is
(a) 2
(b) 1
(c) 0
(d) 0.1
Soln :- (b) 1.
11. The value of 9 sec260°-9 tan2 60° is
(a) 9/2
(b) 3
(c) 18
(d) 9
Soln :- 9 sec260°-9 tan2 60°
= 9 x 22 – 9 x (√3)2
= 9 x 4 – 9 x 3
= 36 – 27
= 9
Hence, The Answer is = (d) 9.
12. Two cubes cach of volume 64 cm3 are joined end to end. Then the surface area of the resulting cuboid is
(a) 128 cm2
(b) 176 cm2
(c) 160 cm2
(d) 192 cm22
Soln :- Let, The length of each cube is x
∴ According to the question,
x3 = 64
⇒ x = 4
Now, The new length of the Combined cube is 4 + 4 = 8
Breath(b) = 4 cm.
Height (h) = 4 cm.
∴ The surface area of the resulting cuboid is 2 (lb + bh +lh)
= 2 (8 X 4 + 4 X 4 + 8 X 4)
= 2 ( 32 + 16 + 32)
= 2 X 80
= 160 cm2
Hence, The answer is (c) 160 cm2.
SECTION-B
13. Prove that 3√2 is irrational.
Soln :- Let us assume to the contrary, that 3√2 is rational.
That is, We can find co-prime a and b (b≠0) such that
Since, 3, a and b are integers, a/3b is rational and so √2 is rational.
But this contradicts the fact that √2 is irrational.
So, We conclude that 3√2 is irrational.
14. Find the 10th term of the following arithmetic progression :
2, 7, 12, …..
Soln :- Here, a = 2, d = 7-2 = 5 and n = 10
We know, an = a + (n-1)d
∴ a10 = 2 + (10-1)x 5
= 2 + 45
= 47
So, the 10th term of the AP:- 2,7,12 …… is 47.
15. Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Soln :- Internally in the ratio m1 : m2. Using the section formula we get,
We know, if x, y = (a, b) then x = a, y = b
Therefore,
= ![]()
⇒ 6m1 + m1 = -m2 + 3m2
⇒ 7m1 = 2m2
⇒ m1:m1 = 2:7
So, the ratio is 2:7.
16. show that
cos38° cos52° – sin38° sin52° = 0
Soln :- L.H.S. = cos38° cos52° – sin38° sin52°
= cos(90° – 52°) cos(90° – 38°) – sin38° sin52°
= sin52° sin38° – sin38° sin52°
= 0
= R.H.S.
17. In ΔABC, ∠B = 90° and tanA = 1. Then show that 2sinA cosA = 1.
Soln :- Here,
L.H.S = tan A = 1
⇒ tan A = tan 45°
![]()
![]()
Again,
![]()
![]()
![]()
![]()
18. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting a spade.
Soln :- There are 4 aces in a deck. Let E be the event ‘the card is an ace’.
The number of outcomes favorable to E = 4
The number of possible outcomes = 52.
We know,
![]()
![]()
19. Prove that
![]()
Soln :-
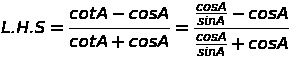
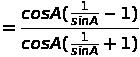
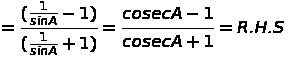
SECTION-C
20. Find the zeros of the quadratic polynomial x2 + 7x + 10 and verify the relationship between the zeros and the coefficients.
Soln :-
Here, x2 + 7x + 10 = 0
⇒ x2 + 2x + 5x + 10 = 0
⇒ x( x + 2 ) + 5( x + 2 ) = 0
⇒ ( x + 2 )( x + 5 )= 0
Either, or,
x + 2 = 0 x + 5 = 0
⇒ u = -2 ⇒ x = -5.
∴ The zeros of x2 + 7x + 10 = 0 are = -2, -5
Now,
Sum of zeros of = -2 + (5) = -7
![]()
And, Product of zeros ,
![]()
Or
Divide 2x2 + 3x + 1 by x + 2.
21. For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7 (a – b)x+(a + b)y = 3a + b – 2
22. Find the roots of the following quadratic equation
2x2 – 2√2x + 1 = 0
Soln :-
Here, a = 2, b = – 2√2 and c = 1
So, b2 – 4ac = 8 – 8 = 0
Therefore,
![]()
So, the roots are ,
![]()
23. Find the value of k for the following quadratic equation, so that it has two equal roots
2x2 + kx + 3 = 0
24. Find the sum of the first 24 terms of the list of numbers whose nth term is given by
an = 3 + 2n.
Soln :-
an = 3 + 2n
a1 = 3 + 2 x 1 = 5
a2 = 3 + 2 x 2 = 7
a3 = 3 + 2 x 3 = 9
List of numbers becomes 5, 7, 9, 11 …..
Here, 7 – 5 = 9 – 7 = 11 – 9 = 2
Therefore, d = 2
To find S24, we have n = 24, a = 5, d = 2
![]()
So, the sum of the first 24 terms of the list of numbers is 672.
25. If the line segment XY is parallel to side AC of ΔABC and it divides the triangle in two parts of equal areas, then find XB / AB.
26. Find the value of k if the points A(2, 3), B(4, k) and C(6, -3) are collinear
27. Find the area of the shaded region in the given figure, where ABCD is a square of side 14 cm:

SECTION-D
28. Solve the following pair of equations by reducing them to a pair of linear equations :

Or
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If the length is increased by 3 units and breadth by 2 units, the area is increased by 67 square units. Find the length and breadth of the rectangle.
29. In an equilateral triangle ABC, D is a point on side BC, such that BD = 1/3BC. Prove that 9AD2 – 7AB2
30. From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the bank, find the width of the river
31. From an external point T, two tangents TP and TQ are drawn to a circle having its centre at O. Prove that ∠PTO = 2∠OPQ.
32. Construct a triangle similar to a given triangle ABC with its sides equal to 3/4 of the corresponding sides of the triangle ABC. (Write the steps of construction.)
SECTION-E
33. A hemispherical tank full of water is emptied by a pipe at the rate of 3×4/7 liters per second. How much time will it take to empty half the tank, if it is 3 m in diameter?
Or
How many silver coins, 1-75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 55cm x 10cm×35cm ?
34. The following table shows the ages of the patients admitted to a hospital for a year. Find the mode and mean of the given data. Compare and interpret the two measures of central tendency?

*****The End****


I gave this exam and this question is comparatively much easier than the CBSE board Question Papers so I would request the authority to higher the level of questions in the boards exam especially mathematics.
Sir,can you please! upload the last 10 years that is from(2007-2018) previous question papers with solution for hslc seba
Thank you for contacting us.
We want to inform you that we are working on it, soon we’ll upload question.
So stay with us and keep supporting
[…] Click here to view General Mathematics Question Paper 2018 […]